Bernoulli trial

In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure".

In practice it refers to a single experiment which can have one of two possible outcomes. These events can be phrased into "yes or no" questions:

Did the coin land heads?
Was the newborn child a girl?

Therefore success and failure are labels for outcomes, and should not be construed literally. Examples of Bernoulli trials include

Flipping a coin. In this context, obverse ("heads") conventionally denotes success and reverse ("tails") denotes failure. A fair coin has the probability of success 0.5 by definition.
Rolling a die, where a six is "success" and everything else a "failure".
In conducting a political opinion poll, choosing a voter at random to ascertain whether that voter will vote "yes" in an upcoming referendum.

1 Definition
2 Example: Tossing Coins
- 2.1 Solution
3 References
4 See also

Definition

Independent repeated trials of an experiment with two outcomes only are called Bernoulli trials. Call one of the outcomes success and the other outcome failure. Let $p$ be the probability of success in a Bernoulli trial. Then the probability of failure $q$ is given by

$q = 1 - p$ .

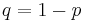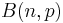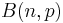A binomial experiment consisting of a fixed number $n$ of trials, each with a probability of success $p$ , is denoted by $B(n,p)$ . The probability of exactly $k$ successes in the experiment $B(n,p)$ is given by:

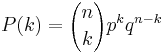$P(k)={n \choose k} p^k q^{n-k}$ .

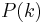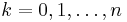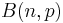The function $P(k)$ for $k=0,1,\ldots,n$ for $B(n,p)$ is called a binomial distribution.

Bernoulli trials may also lead to negative binomial, geometric, and other distributions as well.

Example: Tossing Coins

Consider the simple experiment where a fair coin is tossed four times. Find the probability that exactly two of the tosses result in heads.

Solution

For this experiment, let a heads be defined as a success and a tails as a failure. Because the coin is assumed to be fair, the probability of success is 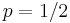$p = 1/2$ . Thus the probability of failure is given by

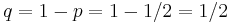$q = 1 - p = 1 - 1/2 = 1/2$ .

Using the equation above, the probability of exactly two tosses out of four total tosses resulting in a heads is given by:

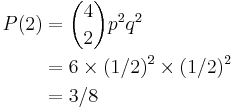$\begin{align} P(2) &= {4 \choose 2} p^2 q^2 \\ &= 6 \times (1/2)^2 \times (1/2)^2 \\ &= 3/8 \end{align}$ .

References

Weisstein, Eric W., "Bernoulli Trial" from MathWorld.

Bernoulli trial

Contents

Definition

Example: Tossing Coins

Solution

References

See also